The below post will be talking in the context of 32-bit ARMv7.
A video that supplements this content can be found here: https://youtu.be/4PmjTFgEybI
Those familiar with the 'Immediate' form of many ARM instructions may know that these 12 bits to encode the immediate value aren't as simple as it may seem at first glance. For a point of reference, we will use the MOV instruction as an example, as in MOV r0, #1337.
The above MOV example is a great one to work with, because it doesn't actually exist, though in this case, your assembler probably wouldn't give you an error, it would just use the word-sized version of MOV (MOVW r0, #1337).
But 12 bits contains 4096 values doesn't it? It could, but the 12-bit immediate field isn't that flat. Again, this is still probably not a new thing to ARM veterans. The 12-bit field is divided into two different parts: the first 4 bits are dedicated to a field that specifies how many times to rotate-right the last 8 bits. So if you specify in the first 4 bits not to rotate at all, then the last 8 bits can be interpreted literally. The 4 bits for rotating right are in multiples of twos, meaning that 0010 means rotate right by four, or 0101 would mean rotate right by ten). In this context, the rest of this post attempts to address the following type of question: "Is 2684354500 easily encode-able, if not, what are the closest numbers surrounding it?"
Why would the architects complicate things so much like this? Well this method does make it easy to load a wide range of larger numbers into a 32-bit register. Otherwise, it kind of sucks to only be able to load a 12-bit number into a 32-bit register. And we can't directly load 32-bit numbers encoded into an instruction, because the instructions themselves are exactly 32-bits, meaning the immediate value would take up all of the space leaving none for the instruction itself.
Let's look at some 12-bit examples:
000000001010
This one is simple, the first four bits don't have any rotation, and the last 8 bits equate to 10 (0xA), so that is the value that would be used.
001000001010
We still have 10 for our last 8 bits, but now our rotate right value is 0010, which means that we will rotate 10 (as a 32 bit value) to the right by four places. So 0x0000000A would then be 0xA0000000, which is a much larger value in decimal (2,684,354,560).
This is the type of thing that means that an instruction like 'MOV r0, #2684354560' is completely valid. On the other hand, 'MOV r0, #2684354500' is not valid. The distinction is unfortunately not super obvious to the naked eye.
Before digging into types of solutions to this issue, I would like to take a small detour about the range of possible numbers you can use, as the behavior here is incredibly interesting in my opinion. Due to the power of rotating bits around, you really can use numbers anywhere from zero to 4 billion and some change, with only 12-bits, or 4,096 possible values. Did I say 4,096 values? this is not true either! There are redundancies, we can rotate one 8-bit value by a certain amount that has the same result of rotating a different 8-bit value by a different amount (we will circle back to this soon). In reality, 25% of these encodings are redundant. There are only 3,073 unique values after eliminating redundancies.
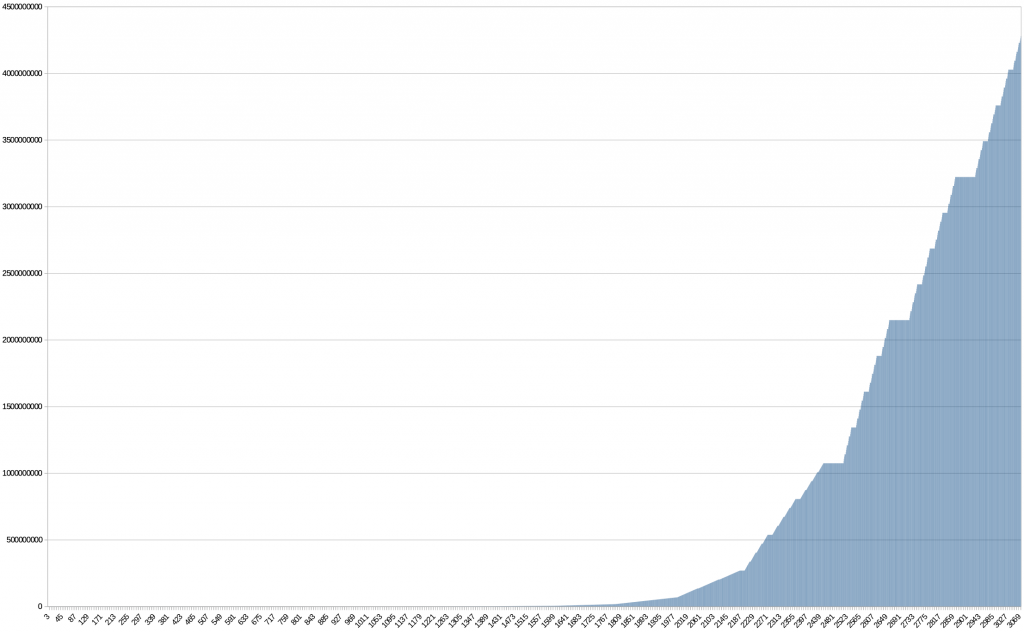
We might also have some intuition that the spread of numbers isn't linear. As in we should know we can literally use values 0-255 with no issue (as we have an un-rotated version of the first 8-bits). Starting at 256 we start counting in fours; as in 256, 260, 264, etc. After 1,024 we start counting in 16's and so on. However, if graphed, the result isn't as exponential as one would expect. There are clusters of numbers that hover on the incrementing by 1 for some stretches, conveniently around half way through as well (two billion and some change). I say conveniently because this allows us to capture small 2's compliment negative numbers. As in, all of these unsigned numbers 2147483648-2147483711 (0x80000000 - 0x8000003F), can be encoded without modification. So this gives us a run of about the first 64 negative integers, not bad. Below is a graph of this spread:
Because redundant. Though it does turn out that there is corresponding assembly for these redundant forms that achieve the same thing (due to some syntactical sweetness). Let's look at an example of MOVing 192 into r0. This can be done vanilla with just 'MOV r0, #192'. The 12-bit encoded value would be 0x0c0. But there are other ways. We could encode 3 into the 8-bit part of the 12-bit encoding and '0xd' into the ROR 4-bit field; which effectively rotates the value 3 in a 32-bit field to the right by 26 places (0xd03). The result is 192. We could also rotate 12 to the right by 28 places (0xe0e). Finally, we could rotate 48 to the right by 30 places to get 192 (0xf30).
In the ARM manual, the syntax for this MOV instruction is: MOV{S}<c> <Rd>, #<const>
To break this down, the {S} is a 1-bit field that specifies if we want to set any conditional flags. The <c> is a 4-bit field specifying under which condition to execute MOV, if you don't include this, the default is to execute under any condition. <Rd> is the destination register that you want your result value stored in. Finally, #<const> is the number you want placed into Rd. What isn't shown for the syntax in this part of the manual (though I remember reading elsewhere in the manual that you can do this) is that you can also specify the ROR value that you want. I would revise the syntax to: MOV{S}<c> <Rd>, #<const>, ror_amount for my own personal use.
All of the below assembly instructions are valid and all achieve the same thing:
mov r0, #192 @e3a000c0
mov r0, #3, 26 @e3a00d03
mov r0, #12, 28 @e3a00e0c
mov r0, #48, 30 @e3a00f30
So say your in a situation where you want to move an immediate large value into a register, but you don't have a good idea of if it is compatible with this format? There are plenty of unsatisfying answers to this question online. Although I probably spent more time on this blog post than I did researching good solutions to this issue. I'll talk about some of the different approaches I have seen to this issue, including my own approach and my own tool.
One of the first resources I came across was https://alisdair.mcdiarmid.
Next up, you will likely find numerous scripts that will take your number as an input and tell you whether or not the number is encodable. I feel like this kind of a tool is a complete waste of my time. Why? I can just try writing 'MOV r0, #2684354500' in assembly, and my assembler will quickly tell me "Error: invalid constant (9fffffc4) after fixup" and at which line this was found. This kind of tool also doens't give me context as to which numbers I CAN use that are close to this one.
There's another approach that kind of side-steps my question altogether. What I like about it is that it is consistent and you don't have to worry about post-processing the number to get it to fit. This solution is to put the number in a .data section and ldr it. What isn't immediately obvious about this solution, however, is that it takes up more data than it first appears.
The number in the data section itself takes up 32 bits. As far as the assembly goes, you need 2 instructions: one to load the pointer address ('ldr r0, =pointer'), and another to de-reference it ('ldr r0, [r0]'). That's another additional 64-bits of data. However, there's another 32-bits that are needed for something way less obvious. In the encoding of this ldr instruction, it always de-references; there's no such thing as ldr just getting a pointer. In actuality, the assembler itself does some behind the scenes magic. At the end of you're .txt section, the address for 'pointer' (or whatever you name it), will be stored. The instruction 'ldr r0, =pointer' replaces =pointer to that end of .txt address, which contains the real pointer. In that context, 'ldr r0, =pointer' is still dereferencing and getting a value, it's just that this value is an address for the value you really want.
In conclusion of this method, it takes 16 bytes (equivalent of 4 instructions) to achieve loading any arbitrary value into a register. The benefit of this instruction is that it is easy and consistent (in both the instructions used and the size taken). Though it consumes 16 bytes of data, run-time only requires 2 instructions of execution (although they are memory operations).
This is my favorite method when it makes sense to use it. This method involves moving the closest valid number to the one you want to move into a register and then using an ADD or SUB to make up for the difference.
There are challenges to this though. First, it's not readily easy (without some kind of tool) to just guess what the next closest encodable number is to the number you want. Next, it is also possible that the number it would take to ADD or SUB to get to your number is also not encodable, meaning you may have to do more than one ADD or SUB. Finally, and related to the previous point, if you hit a point where you're doing 4 or more ADD/SUB operations, you would be taking up more disk space than the LDR method. Additionally, it's not only 4 instructions worth of storage, but 4 instructions executed too, however, these are all direct register operations (quicker).
Why do I prefer this method? Assuming I'm not going to have to deal with all of these annoying calculations myself, I like the elegance of it, subjective, I know. But I like that all the information regarding this operation is all right there in-line. I don't have to refer to a .data section. It also usually takes up less space than the LDR method. The space savings may not be enough to justify for some, but less space is less space. However, if I didn't have some external tool to make this process easy, I would probably just be lazy and use the LDR method.
Regarding the following question: "Is 2684354500 easily encodable, if not, what are the closest numbers surrounding it?" I wrote a tool to answer this question and additionally suggest a solution to the Post Processing method. I was going to write this tool in a high level scripting language like a bitch, but then decided to write it in ARM assembly.
The tool is called ImmSuggest, it takes one argument; the number you want to encode. If the number is encodable, it just gives an example instruction such as 'mov r0, #200' (assuming your number was 200).
If your number is not encodable, the tool will display your number surrounded by the next lowest and highest number that is encodable. Next it gives a series of instructions that would get your number into register r0 with a MOV and ADD instructions. For example, say you wanted to encode 301 (not encodable), the output of the tool would look like this:
300 < 301 > 304
mov r0, #300
add r0, #1
300 is encodable, so is 304. If those numbers are good enough for you for your use-case, you can just choose one of those instead. Otherwise, move 300 into your register, and then just add 1 to it.
Again, our question: "Is 2684354500 easily encodable, if not, what are the closest numbers surrounding it?"
./ImmSuggest 2684354500
2667577344 < 2684354500 > 2684354560
mov r0, #2667577344
add r0, #16711680
add r0, #65280
add r0, #196
Note, this isn't perfect at all, which is nice that it also displays the surrounding closest numbers for us. I say that because you may notice that the number we want to encode is actually only 60 away from the next highest encodable integer. This means that the following code would also work:
mov r0, #2684354560
sub r0, #60
For simplicity, I wanted to just keep this to MOV and ADD instructions. I thought about doing a series of the most efficient combination of ADD and SUB instructions, but it weirdly got more complicated than I felt dealing with. Especially with the limitations I gave myself.
This is all self-imposed, hence why stupid. This program is about 16k and runs pretty fast. I know, it would run fast in perl/python/ruby/etc as well, as it's not that complicated. I mostly chose the challenge of writing this in assembly, since it is about assembly. I also tried to be pure and not rely on external libraries (notably libc).
This is often a mutually exclusive trade-off and this program is no exception. Where this really stands out is that I pre-generated a header file that contains a sorted list of all 3,073 valid encodable integers. This is about 80% of the resulting program. The program could be significantly smaller if it just dynamically generated all of these values and put them into memory, however, this would also add a lot of cycles that would be executed every single time the program is run. With the pre-computed header file, this needs to be done none of the times.
Even though I have been using the libc library from assembly quit a bit lately, I decided to throw away all of its usefulness and overhead and only rely on Linux API functionality to do my work. Just linking with gcc costs 3,000 instructions of execution, and then another 1,000 instructions of execution for the first time of use of any function (your printf's, malloc's, isupper's, etc...). Granted, either strategy of whether to use libc or not will still result in this program executing in an un-noticable fraction of a second, my version currently executes in anywhere from about 325 - 6900 instructions (depending on how large the argument is; as this affects how complicated the result is).
In other words, on average, this program finishes before a gcc linked executable would even be done loading it's functions. If you use more than 4 libc functions (printf, malloc, getopt, etc...), youre libc overhead already runs slower than even the worst case run of my program. In a best case run of my program, a gcc linked program wouldn't have even gotten to your part of the code (main function) yet. Don't get me wrong, I don't hate libc, and I understand much of the benefits of dynamic linking of shared libraries. But I also rage when I see shit like this: https://stackoverflow.com/questions/3233560/in-c-is-it-faster-to-use-the-standard-library-or-write-your-own-function (honest question, naive and misled text-book answers). So I guess what I'm trying to say is I wrote my program this way out of principle.
Throughing away libc brings challenges though, even the simplest things. For example, I want to print the value of a register to stdout, but as an ASCII decimal number. Printf would make that effortless, but I'm not using printf. One good way to get a decimal equivalent is to massage the data through many rounds of div by 10 and extracting the modulus values. This is all and good, but my Raspberry Pi doesn't support the div instruction. The code for this actually has to be written as well. I cheated with this a little, by manually 'statically' including a version of divsi3 from libc (as it both does division and keeps the remainder). Though halfway through modifying divsi3 to my needs, I realized it worked on signed values instead of unsigned. And the udivsi3 function didn't seem to capture the remainders of the divs. So I just kind of strategically commented out most of the rsb (negate) instructions from divsi3 and things worked out.
Getting an argument from stdin was actually pretty easy, as arguments are on the stack. Converting the ASCII number to a register value takes more work than acquiring it from the stack.
Therez none. If you supply an integer too large (to fit in 32 bits), you'll get stupid answers back. If it's not an integer, stupid crap back. If it's not even a number, stupid crap. I removed the div by 0 error checking in the soft division routine, I'm always dividing by 10. I hope that decision enrages at least one person.
So you know, do this, I don't care:
./ImmSuggest burgers
57409536 < 57621027 > 57671680
mov r0, #57409536
add r0, #210944
add r0, #544
add r0, #3